前言
在字符串匹配问题中,有很多经典算法。其中,KMP算法是单模字符串匹配的“终极”算法。
KMP算法是根据三位作者(D.E. Knuth、J.H. Morris、V.R. Pratt)的名字来命名的,算法全称为 Knuth Morris Pratt 算法,简称KMP算法。
问题简述
单模字符串匹配,指的是一个字符串 $a$ 和一个字符串 $b$ 进行匹配,$a$ 的长度远大于 $b$,需要查找在 $a$ 中是否包含 $b$。其中 $a$ 称为主串,$b$ 称为模式串。
问题分析
我们能想到的最简单的办法,就是模式串在主串中滑动,从前往后依次查看有没有匹配的串。如下图: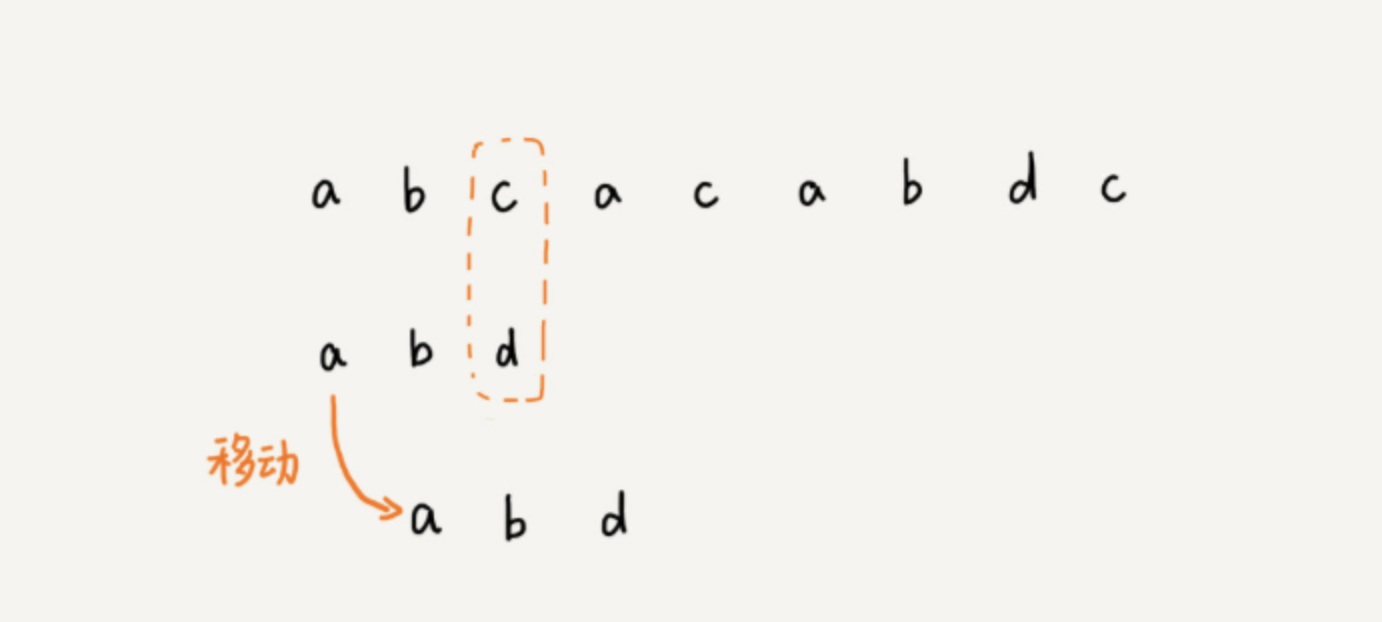
这种算法称为BF算法,或朴素匹配算法。算法的最坏时间复杂度为 $O(n*m)$,其中 $n$ 为主串长度,$m$ 为模式串长度。
下面,我们思考一个问题:在遇到不匹配的字符时,我们只是把模式串向后移动一位,是不是效率低了?有没有办法让模式串多向后移动几位?KMP算法,正是基于这个初衷,提出来的。
坏字符与好前缀
在介绍KMP算法之前,我们先介绍一些前置概念。
如下图,在主串和模式串匹配过程中,遇到的不能匹配的字符,我们称之为坏字符。相应的,我们把坏字符前,已经匹配的前缀子串称为好前缀。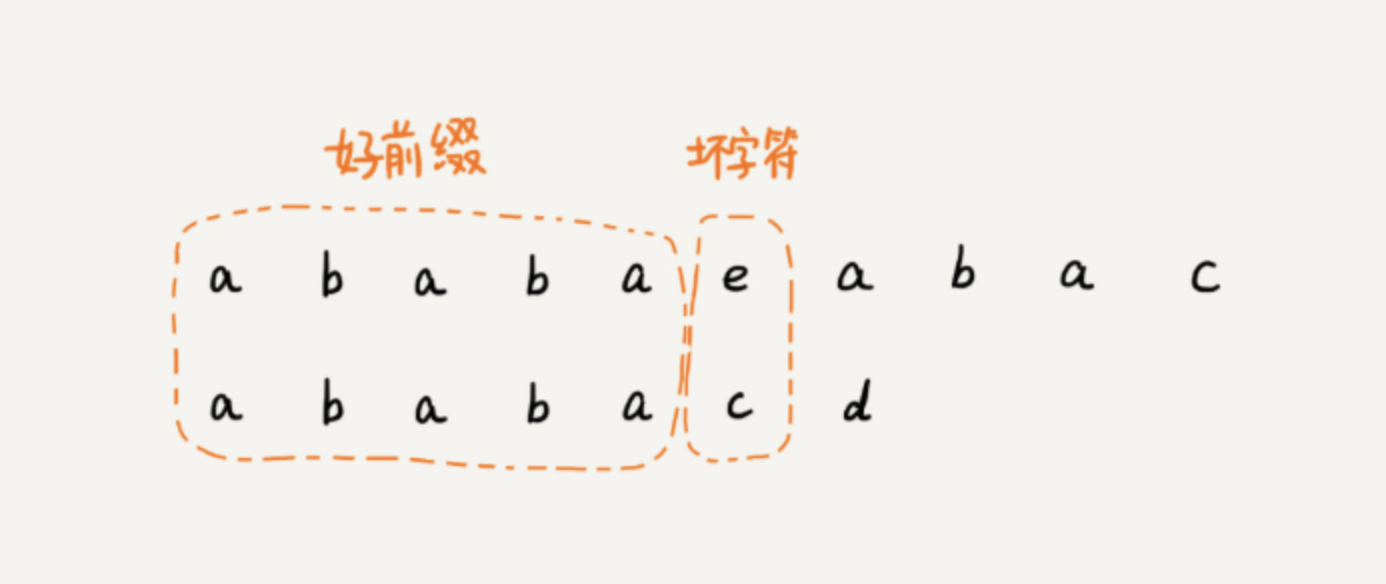
模式串滑动
我们知道,当我们遇到坏字符时,意味着模式串需要向后滑动。那么,我们最多可以滑动多少位呢?
如下图,我们可以考察好前缀的后缀子串与模式串的前缀子串,找到好前缀的后缀子串中,最长的能够与模式串前缀子串匹配的串,然后进行滑动(可以思考下,为什么要求是最长子串?如果不是最长子串,有可能滑动位数过多,导致不能覆盖全部情况,导致漏匹配)。注意,由于此时模式串的前缀子串=好前缀的前缀子串,故我们可以换一种说法,即找到好前缀的后缀子串中,最长的能够与好前缀的前缀子串匹配的串,然后进行滑动。像图中的情况,我们就可以把模式串向后滑动2位。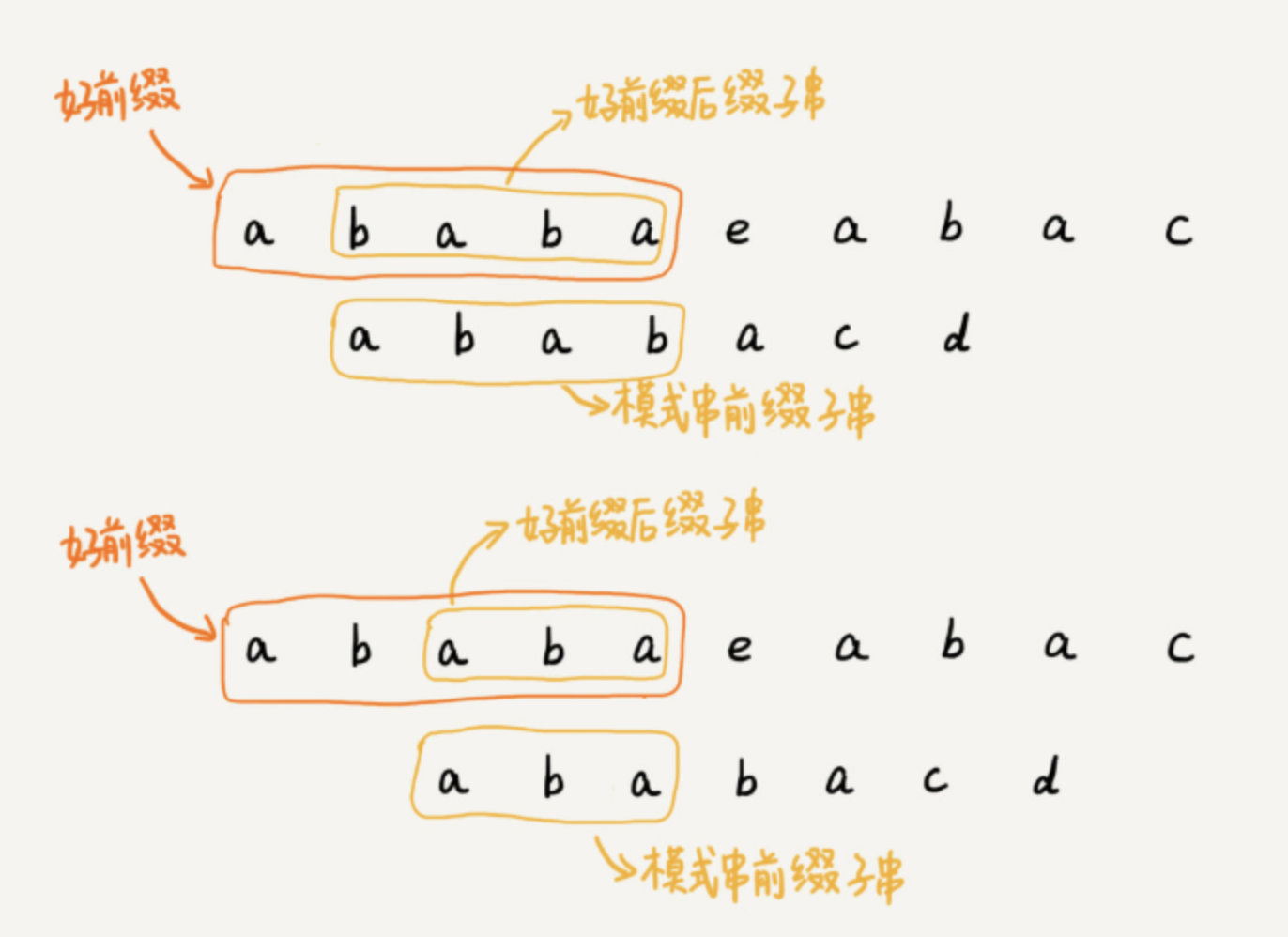
一般的,假设坏字符在主串中的位置为 $i$,在模式串中的位置为 $j$,好前缀的最长可匹配前后缀子串(字符串中,前缀子串与后缀子串的最长匹配串)长度为 $k$,那么,我们需要把模式串向后滑动 $j-k$ 位,并从模式串的 $k+1$ 位开始,继续进行匹配。如下图:
next数组
我们发现,可以预先根据模式串,求得各前缀的最长可匹配前后缀子串,记录最长前缀子串的位置,存储在数组中,再和主串进行匹配,快速得到匹配结果。我们把这个数组定义为next数组,很多地方也把这个数组定义为失效函数。
数组的下标是每个前缀结尾字符的下标,数组的值为该前缀的最长可匹配前后缀子串中,前缀子串结尾字符的下标,相当于前缀子串长度 $k$ 减去1。下图为一个例子:
next数组的求解
next数组的求解,我们可以利用动态规划的思想。我们知道,对于动态规划,最重要的是找到状态和状态转移方程。在本例中,状态是数组中的值,即模式串每个前缀的最长可匹配前后缀子串中前缀子串的位置。对于状态转移方程,要求得模式串 $b$ 中,第 $i$ 个字符的next值,即 $next[i]$,我们可以先假设已经求得了 $next[0]…next[i-1]$,且 $next[i-1]=k-1$,即子串 $b[0, k-1]$ 是 $b[0, i-1]$ 的最长可匹配前后缀子串。下面,我们分类讨论:
- 如果 $b[k]=b[i]$,即 $b[k-1]$ 的下一个字符等于 $b[i-1]$ 的下一个字符,那么,我们可以马上得出结论:$b[0, k]$ 即为 $b[0, i]$ 的最长可匹配前后缀子串,$next[i]=k$。
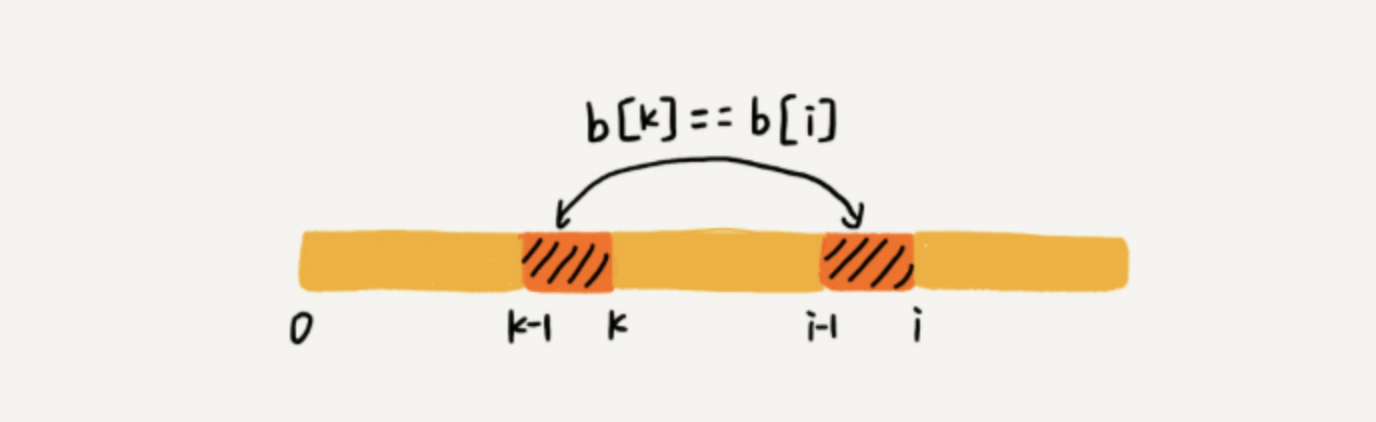
- 如果 $b[k]!=b[i]$,即 $b[k-1]$ 的下一个字符不等于 $b[i-1]$ 的下一个字符。则我们需要找到 $b[0, k-1]$ 的最长前缀子串 $b[0, l]$,且该串最后一个字符的下一个字符为 $b[i]$,即 $b[l+1]=b[i]$。这个时候,我们可得到 $next[i]=l+1$。
问题解决
我们先给出框架代码如下:
next数组的求解属于比较难理解的部分,代码如下:
由上述代码可知,KMP算法的时间复杂度为 $O(n+m)$,即两个串都遍历一遍即可;空间复杂度为 $O(m)$,需要申请一个和模式串长度一样的数组。其中 $n$ 为主串长度,$m$ 为模式串长度。
参考资料
字符串匹配1———单模式匹配(BF,RK,Sunday,BM,KMP)

